History of mathematical notation
Mathematical notation comprises the symbols used to write mathematical equations and formulas. It includes Hindu-Arabic numerals, letters from the Roman, Greek, Hebrew, and German alphabets, and a host of symbols invented by mathematicians over the past several centuries.
The development of mathematical notation for algebra can be divided in three stages. The first is "rhetorical", where all calculations are performed by words and no symbols are used. Most medieval Islamic mathematicians belonged to this stage. The second is "syncopated", where frequently used operations and quantities are represented by symbolic abbreviations. To this stage Diophantus belonged. The third is "symbolic", which is a complete system of notation replacing all rhetoric. This system was in use by medieval Indian mathematicians and in Europe since the middle of the 17th century.[1]
(See table of mathematical symbols for a list of symbols.)
Contents |
Beginning of notation
Written mathematics began with numbers expressed as tally marks, with each tally representing a single unit. For example, one notch in a bone represented one animal, or person, or anything else. The symbolic notation was that of the Egyptians. They had a symbol for one, ten, one-hundred, one-thousand, ten-thousand, one-hundred-thousand, and one-million. Smaller digits were placed on the left of the number, as they are in Hindu-Arabic numerals. Later, the Egyptians used hieratic instead of hieroglyphic script to show numbers. Hieratic was more like cursive and replaced several groups of symbols with individual ones. For example, the four vertical lines used to represent four were replaced by a single horizontal line. This is first found in the Rhind Mathematical Papyrus. The system the Egyptians used was discovered and modified by many other civilizations in the Mediterranean. The Egyptians also had symbols for basic operations: legs going forward represented addition, and legs walking backward to represent subtraction.
Like the Egyptians, the Mesopotamians had symbols for each power of ten. Later, they wrote their numbers in almost exactly the same way done in modern times. Instead of having symbols for each power of ten, they would just put the coefficient of that number. Each digit was at first separated by only a space, but by the time of Alexander the Great, they had created a symbol that represented zero and was a placeholder. The Mesopotamians also used a sexagesimal system, that is base sixty. It is this system that is used in modern times when measuring time and angles.
Greek notation
The Greeks at first employed Attic numeration, which was based on the system of the Egyptians and was later adapted and used by the Romans. Numbers one through four were vertical lines, like in the hieroglyphics. The symbol for five was the Greek letter pi, which is the first letter of the Greek word for five, pente. (This is not to be confused with the modern constant also denoted by, and referred to as "pi," which is a constant equal to the ratio of the diameter of a circle to its circumference. Greek mathematicians did not have a formal name for what we now know as "pi," and certainly did not associate their letter pi, equivalent to "P" in English, with it.) Numbers six through nine were pente with vertical lines next to it. Ten was represented by the first letter of the word for ten, deka, one-hundred by the first letter from the word for one-hundred, etc.
The Ionian numeration used the entire alphabet and three archaic letters.
| Α (α) | Β (β) | Г (γ) | Δ (δ) | Ε (ε) | Ϝ (ϝ) | Z (ζ) | H (η) | θ (θ) | I (ι) | K (κ) | Λ (λ) | Μ (μ) | Ν (ν) | Ξ (ξ) | Ο (ο) | Π (π) | Ϟ (ϟ) | Ρ (ρ) | Σ (σ) | Τ (τ) | Υ (υ) | Ф (φ) | Χ (χ) | Ψ (ψ) | Ω (ω) | Ϡ (ϡ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
This system appeared in the third century BC, before the letters digamma (Ϝ), koppa (Ϟ), and sampi (Ϡ) became archaic. When lowercase letters appeared, these replaced the uppercase ones as the symbols for notation. Multiples of one-thousand were written as the first nine numbers with a stroke in front of them; thus one-thousand was, α, two-thousand was, β, etc. M was used to multiply numbers by ten-thousand. The number 88,888,888 would be written as M,ηωπη*ηωπη[2]
Greek mathematical reasoning was almost entirely geometric (albeit often used to reason about non-geometric subjects such as number theory), and hence the Greeks had no interest in algebraic symbols. The great exception was Diophantus of Alexandria the first great algebraists. His Arithmetica was one of the first texts to use symbols in equations. It was not completely symbolic, but was much more than previous books. An unknown number was called s. The square of s was 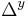 ; the cube was
; the cube was 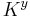 ; the fourth power was
; the fourth power was 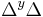 ; and the fifth power was
; and the fifth power was 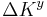 . The expression
. The expression 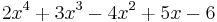 would be written as SS2 C3 x5 M S4 u6.
would be written as SS2 C3 x5 M S4 u6.
Chinese notation
The Chinese used numerals that look much like the tally system. Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the Roman numeral for ten. Nowadays, the huāmǎ system is only used for displaying prices in Chinese markets or on traditional handwritten invoices.
Indian notation
The algebraic notation of the Indian mathematician, Brahmagupta, was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms.[3]
Beginning of Hindu-Arabic numerals
Despite their name, Arabic numerals actually started in India. The reason for this misnomer is Europeans first saw the numerals used in an Arabic book, Concerning the Hindu Art of Reckoning, by Mohommed ibn-Musa al-Khwarizmi. Al-Khwarizmi did not claim the numerals as Arabic, but over several Latin translations, the fact that the numerals were Indian in origin was lost.
One of the first European books that advocated using the numerals was Liber Abaci, by Leonardo of Pisa, better known as Fibonacci. Liber Abaci is better known for the mathematical problem Fibonacci wrote in it about a population of rabbits. The growth of the population ended up being a Fibonacci sequence, where a term is the sum of the two preceding terms.
North African notation
Abū al-Hasan ibn Alī al-Qalasādī (1412–1482) was the last major medieval Arab algebraist, who improved on the algebraic notation earlier used in the Maghreb by Ibn al-Banna in the 13th century[4] and by Ibn al-Yāsamīn in the 12th century. In contrast to the syncopated notations of their predecessors, Diophantus and Brahmagupta, which lacked symbols for mathematical operations,[5] al-Qalasadi's algebraic notation was the first to have symbols for these functions and was thus "the first steps toward the introduction of algebraic symbolism." He represented mathematical symbols using characters from the Arabic alphabet.[4]
Pre-calculus
Two of the most widely used mathematical symbols are addition and subtraction, + and −. The plus sign was first used by Nicole Oresme in Algorismus proportionum, possibly an abbreviation for "et", which is "and" in Latin (in much the same way the ampersand began as "et"). The minus sign was first used by Johannes Widmann in Mercantile Arithmetic. Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively.[6] The radical symbol 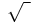 for square root was introduced by Christoph Rudolff because it resembled a lowercase "r" (for "radix").
for square root was introduced by Christoph Rudolff because it resembled a lowercase "r" (for "radix").
In 1557 Robert Recorde published The Whetstone of Witte which used the equal sign (=) as well as plus and minus signs for the English reader. The New algebra (1591) of François Viète introduced the modern notational manipulation of algebraic expressions. In 1631 William Oughtred introduced the multiplication sign (×) and abbreviations sin and cos for the trigonometric functions.
William Jones used π in Synopsis palmariorum mathesios in 1706 because it is the first letter of the Greek word perimetron (περιμετρον), which means perimeter in Greek. This usage was popularized by Euler in 1737.
Calculus
Calculus had two main systems of notation, each created by one of the creators: that developed by Isaac Newton and the notation developed by Gottfried Leibniz. Leibniz's is the notation used most often today. Newton's was simply a dot or dash placed above the function. For example, the derivative of the function x would be written as 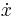 . The second derivative of x would be written as
. The second derivative of x would be written as 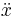 , etc. In modern usage, this notation generally denotes derivatives of physical quantities with respect to time, and is used frequently in the science of mechanics.
, etc. In modern usage, this notation generally denotes derivatives of physical quantities with respect to time, and is used frequently in the science of mechanics.
Leibniz, on the other hand, used the letter d as a prefix to indicate differentiation, and introduced the notation representing derivatives as if they were a special type of fraction. For example, the derivative of the function x with respect to the variable t in Leibniz's notation would be written as 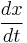 . This notation makes explicit the variable with respect to which the derivative of the function is taken.
. This notation makes explicit the variable with respect to which the derivative of the function is taken.
Leibniz also created the integral symbol, 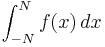 . The symbol is an elongated S, representing the Latin word Summa, meaning "sum". When finding areas under curves, integration is often illustrated by dividing the area into infinitely many tall, thin rectangles, whose areas are added. Thus, the integral symbol is an elongated s, for sum.
. The symbol is an elongated S, representing the Latin word Summa, meaning "sum". When finding areas under curves, integration is often illustrated by dividing the area into infinitely many tall, thin rectangles, whose areas are added. Thus, the integral symbol is an elongated s, for sum.
Euler
Leonhard Euler was one of the most prolific mathematicians in history, and perhaps was also the most prolific inventor of canonical notation. His contributions include his use of e to represent the base of natural logarithms. It is not known exactly why  was chosen, but it was probably because the first four letters of the alphabet were already commonly used to represent variables and other constants. Euler was also one of the first to use
was chosen, but it was probably because the first four letters of the alphabet were already commonly used to represent variables and other constants. Euler was also one of the first to use  to represent pi consistently. The use of
to represent pi consistently. The use of  was first suggested by William Jones, who used it as shorthand for perimeter. Euler was also the first to use
was first suggested by William Jones, who used it as shorthand for perimeter. Euler was also the first to use  to represent the square root of negative one,
to represent the square root of negative one, 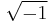 , although he earlier used it as an infinite number. (Nowadays the symbol created by John Wallis,
, although he earlier used it as an infinite number. (Nowadays the symbol created by John Wallis, 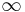 , is used for infinity.) For summation, Euler was the first to use sigma, Σ, as in
, is used for infinity.) For summation, Euler was the first to use sigma, Σ, as in 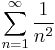 . For functions, Euler was the first to use the notation
. For functions, Euler was the first to use the notation  to represent a function of
to represent a function of  .
.
Peano
In 1895 Giuseppe Peano issued the first edition of his Formulario mathematico, an effort to digest mathematics into terse text based on special symbols. The copy he passed to Bertrand Russell in 1900 at a Paris conference so impressed Russell that he too was taken with the drive to render mathematics more concisely. The result was Principia Mathematica written with Alfred North Whitehead. This treatise marks a watershed in modern literature where symbol became dominant. Peano's Formulario Mathematico, though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4200 formulas and theorems.
Logic
Once logic was recognized as an important part of mathematics, it received its own notation. Some of the first was the set of symbols used in Boolean algebra, created by George Boole in 1854. Boole himself did not see logic as a branch of mathematics, but it has come to be encompassed anyway. Symbols found in Boolean algebra include 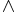 (AND),
(AND), 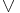 (OR), and
(OR), and 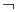 (NOT). With these symbols, and letters to represent different truth values, one can make logical statements such as
(NOT). With these symbols, and letters to represent different truth values, one can make logical statements such as 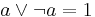 , that is "(a is true OR a is NOT true) is true", meaning it is true that a is either true or not true (i.e. false). Boolean algebra has many practical uses as it is, but it also was the start of what would be a large set of symbols to be used in logic. Most of these symbols can be found in propositional calculus, a formal system described as
, that is "(a is true OR a is NOT true) is true", meaning it is true that a is either true or not true (i.e. false). Boolean algebra has many practical uses as it is, but it also was the start of what would be a large set of symbols to be used in logic. Most of these symbols can be found in propositional calculus, a formal system described as 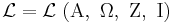 .
. 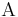 is the set of elements, such as the a in the example with Boolean algebra above.
is the set of elements, such as the a in the example with Boolean algebra above.  is the set that contains the subsets that contain operations, such as
is the set that contains the subsets that contain operations, such as 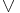 or
or 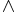 .
. 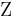 contains the inference rules, which are the rules dictating how inferences may be logically made, and
contains the inference rules, which are the rules dictating how inferences may be logically made, and 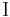 contains the axioms. (See also: Basic and Derived Argument Forms). With these symbols, proofs can be made that are completely artificial.
contains the axioms. (See also: Basic and Derived Argument Forms). With these symbols, proofs can be made that are completely artificial.
While proving his incompleteness theorems, Kurt Gödel created an alternative to the symbols normally used in logic. He used Gödel numbers, which were numbers that represented operations with set numbers, and variables with the first prime numbers greater than 10. With Gödel numbers, logic statements can be broken down into a number sequence. Gödel then took this one step farther, taking the first n prime numbers and putting them to the power of the numbers in the sequence. These numbers were then multiplied together to get the final product, giving every logic statement its own number.[7] For example, take the statement "There exists a number x such that it is not y". Using the symbols of propositional calculus, this would become 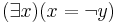 . If the Gödel numbers replace the symbols, it becomes {8, 4, 11, 9, 8, 11, 5, 1, 13, 9}. There are ten numbers, so the first ten prime numbers are found and these are {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving
. If the Gödel numbers replace the symbols, it becomes {8, 4, 11, 9, 8, 11, 5, 1, 13, 9}. There are ten numbers, so the first ten prime numbers are found and these are {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}. Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving 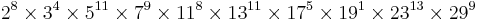 . The resulting number is approximately
. The resulting number is approximately 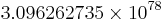 .
.
Notes
- ^ Solomon Gandz. "The Sources of al-Khowarizmi's Algebra"
- ^ Boyer, Carl B. A History of Mathematics, 2nd edition, John Wiley & Sons, Inc., 1991.
- ^ (Boyer 1991, "China and India" p. 221) "he was the first one to give a general solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. [...] It is greatly to the credit of Brahmagupta that he gave all integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India - or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words."
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Qalasadi.html.
- ^ (Boyer 1991, "Revival and Decline of Greek Mathematics" p. 178) "The chief difference between Diophantine syncopation and the modern algebraic notation is the lack of special symbols for operations and relations, as well as of the exponential notation."
- ^ Miller, Jeff. "Earliest Uses of Symbols of Operation." 04 June 2006. Gulf High School. 24 September 2006 <http://jeff560.tripod.com/operation.html>.
- ^ Casti, John L. 5 Golden Rules. New York: MJF Books, 1996.
See also
References
- Florian Cajori (1929) A History of Mathematical Notations, 2 vols. Dover reprint in 1 vol., 1993. ISBN 0486677664.